Ъгълът между равнините
Вид работа: 14
Относно: Ъгълът между самолетите
В ABCDA_1B_1C_1D_1 редовен четириъгълна призма страна на основата 4. страничните ръбове са равни 6. точка М на - CC_1 средата ребро, на BB_1 ръба маркиран N. точка, така че BN: NB_1 = 1: 2.
а) В какъв аспект AMN равнина разделя DD_1 край?
б) Да се намери ъгълът между ABC и AMN равнини.
а) AMN равнина пресича ръба DD_1 К. точка, в която четвъртата връх на напречното сечение на призма равнина. Раздел е успоредник ANMK. поради противоположните страни на призмата са успоредни.
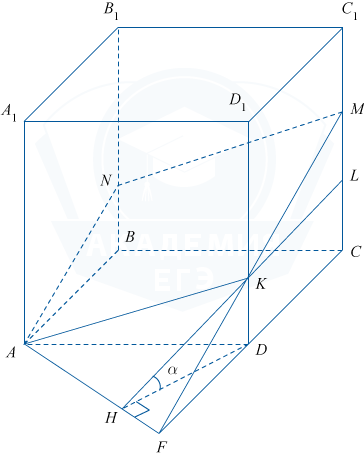
BN = \ frac13BB_1 = 2. Равен KL \ паралелно CD, след това триъгълници ABN и KLM са равни, тогава ML = BN = 2, LC = MC-ML = 3-2 = 1, KD = LC = 1. След KD_1 = 6-1 = 5. Вече можете да намерите съотношението на КД: KD_1 = 1: 5.
б) F - пропускателен пункт на компактдиска линии и KM. ABC и AMN равнини се пресичат в права линия AF. Ъгъл \ ъгъл KHD = \ алфа - линеен двустенен ъгъл (HD \ престъпника AF, тогава теоремата, обратната теоремата на три вертикалите, KH \ престъпника AF). Той е малък ъгъл на правоъгълен триъгълник KHD. катет KD = 1.
Триъгълниците FKD и подобни FMC (KD \ паралелно MC), така FD: FC = KD: MC, решава част FD: (FD + 4) = 1: 3, ние получаваме FD = 2. На правоъгълен триъгълник AFD (\ ъгъл D = 90 ^) с крака 2 и 4 изчисли хипотенузата AF = \ SQRT = 2 \ SQRT 5, DH = AD \ cdot FD: AF = \ Frac = \ frac4.
На правоъгълен триъгълник KHD намери TG \ алфа = \ Frac = \ frac4 следователно желания ъгъл \ алфа = arctg \ frac4.
Вид работа: 14
Относно: Ъгълът между самолетите
Като се има предвид десен квадрат пирамида със странична KMNPQ MNPQ база. равно на 6 и страничен ръб 3 \ SQRT.
а) Изграждане сечение на пирамидата от равнината, минаваща през линия, успоредна на права на диагонал MP на NF. ако точка F - средата на ребро МК.
б) Виж ъгълът между равнината на разреза и KMP.
а) Да KO - височина на пирамидата, F - средата на МК; FE \ паралелно MP (ПКМ в самолет). От FE - средната линия \ триъгълник ПКМ, за FE = \ frac2.

Ние се изгради раздел пирамида равнина, минаваща през и успоредно MP NF. т.е. самолет НВО. L - EF пресечната точка и КО. Тъй като точки L и М принадлежат към желаното напречно сечение и лежат в равнина KQN на. Т. се получава като пресечната точка на LN и KQ. Също така е пресечната точка на желаното напречно сечение и KQ ребрата. NETF - желания участък.
б) равнини на НВТ и MPK пресичат в права линия FE. Следователно, ъгълът между равнините е линейна двустенен ъгъл Ofen. Ние го изгради: LO \ престъпника MP, MP \ паралелно FE, следователно, LO \ престъпника FE; \ Триъгълник НВТ - равнобедрен (NE = NF като съответната Медианата KPN и KMN равни триъгълници). NL - неговата централна (EL = LF, тъй PO = OM и \ триъгълник KEF \ СИМ \ триъгълник KPM). Следователно NL \ престъпника FE и \ ъгъл NLO - потърси.
ON = \ frac12QN = \ frac12MN \ SQRT 2 = 3 \ SQRT 2.
\ Триъгълник KON - правоъгълна.
Питагор крак KO е КО = \ SQRT.
OL = \ frac12KO = \ frac12 \ SQRT = \ frac12 \ SQRT = \ frac12 \ SQRT = \ frac32 \ SQRT = \ frac32 \ cdot 2 \ SQRT 6 = 3 \ SQRT 6.
Вид работа: 14
Относно: Ъгълът между самолетите
ABCDA_B_C_D_ база полето призма е ромб с ъгъл Б. тъп равна на 120 ^ \ Circ. Всички ръбовете на призмата са 10 точки P и K Най - средата CC_ и CD краищата съответно.
а) докаже, че РК и PB_ перпендикулярно.
б) Да се намери ъгълът между самолетите и PKB_ C_B_B.
а) Ние използваме метода на координати. Намери скаларен продукт на вектори \ VEC и \ VEC> и след това косинуса на ъгъла между тези вектори. Изпрати Oy ос заедно CD. Оз ос по CC_ и престъпника компактдиска на оста Ox \. C - произхода.
След C (0, 0, 0); C_ (0; 0; 10); P (0, 0, 5); К (0, 5, 0); B (BC \ COS 30 ^ \ Circ; пр \ грях 30 ^ \ Circ 0), който е В (5 \ SQRT 5 0) B_ (5 \ SQRT 5; 10).
Да предположим, че ъгълът между \ VEC и \ VEC> е \ алфа. \ Cos \ а = 0, тогава \ VEC \ престъпника \ VEC> и директно РК и PB_ перпендикулярно.б) на ъгъла между равнините е равен на ъгъла между ненулеви вектори, перпендикулярна на тези равнини (или, когато тъп ъгъл, съседен на ъгъл от него). Такива вектори са означени като перпендикулярна на равнината. Ние ги намери.
Нека \ ВЕЦ> = \ PKB_ перпендикулярна на плоскостта. Ние го намери, мислейки системата \ започне \ ВЕЦ> \ престъпника \ ВЕЦ, \\ \ ВЕЦ> \ престъпника \ ВЕЦ>. \ крайНека \ ВЕЦ> = \ C_B_B перпендикулярна на плоскостта. Намерете го, мислейки системата \ започне \ ВЕЦ> \ престъпника \ ВЕЦ> \\ \ ВЕЦ> \ престъпника \ ВЕЦ. \ край
\ Започнете 0x + 0y + 10z = 0, 5 \\ \ sqrtx + 5Y + 0z = 0; \ край
Намираме косинус на желания ъгъл \ бета (тя е равна на косинуса на ъгъла между модула \ VEC> и \ VEC>).