Мястото на точки - studopediya
Определение.
Локус точки (наричани HMT), наречен равнина на фигурата, състояща се от точки с определени свойства, а не съдържащи всяка точка, която няма този комплекс.
Ще разгледаме само тези GMT, които могат да бъдат изградени с владетел и компас.
Помислете върху мястото в самолета с най-простите и най-често се изразява имота:
1) локус, разположени на определено разстояние г от тази точка О е окръжност с център в точката на радиус R.
2) на мястото на еднакво разстояние от две точки на данни и В е линия, перпендикулярна на отсечката АВ и минаваща през средата му.
3) локус на еднакво разстояние от две пресичащи се линии за данни имат чифт взаимно перпендикулярни линии, преминаващи през точката на пресичане и разделящи ъглите между права половина.
4) локус, разположени на равни разстояния часа от линията, има две прави линии, успоредни на правата линия и разположени от двете й страни на това разстояние часа.
5) локуса на центровете на кръгове, свързани с линия м в точка М над него, е перпендикулярна на AB в точка М (с изключение на точка М).
6) локуса на центровете на кръгове, свързани с кръга в тази него ochke М, е права линия, минаваща през точка М и центъра на кръга (с изключение на точките М и О).
7) локус от която активният сегмент е видимо под определен ъгъл, от две дъги от окръжности, описани в този интервал и обхващащ определен ъгъл.
8) локус, разстоянието, от което две информационни точки А и В са в съотношение м. п е кръг (наречена Аполоний кръг).
9) локуса на средите на хордите съставени от една точка на кръга е кръга конструирана на сегмент свързваща тази точка до центъра на кръга, като диаметър.
10) локуса на върховете на триъгълници на равно на това и с обща основа, две прави линии е успоредна на земята и преминават през върха на триъгълника и е симетричен по отношение на линията, съдържащ база.
Ето някои примери за намиране на мястото.
Пример 2.Find HMT в средите на акорда съставени от една точка на обиколката (локус № 9).
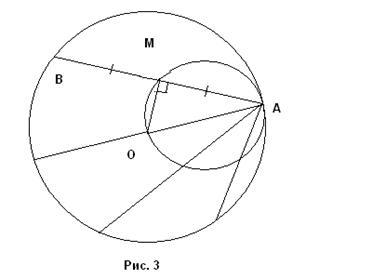
Решение. Предвид окръжност с център О и кръга е избран от точка А, които се държат акорд. Ние показваме, че желаното място е кръг построен на AB като диаметър (с изключение на точка А) (фиг. 3).
Нека AB - определен акорд и М - я средата. Свързване М и О. След IO ^ AB (радиус, хорда разделя на половина, перпендикулярна на тази хорда). Но след това ÐАМО 90 = 0. Следователно М принадлежи кръг с диаметър AB (HMT № 7). защото този кръг минава през точка О, тогава G принадлежи на нашия локус.
От друга страна, предполагам, че М принадлежи на нашия HMT. След това, след като е прекарал през M акорд AB и свързването на М и О, ние откриваме, че ÐАМО = 0. 90 т.е. MO ^ AB, което означава, че M - средата на акорд AB. Ако М съвпада с G, O - AC средата.
координира метод често Ви позволява да намерите мястото на.
Пример 3.Nayti HMT, разстоянието, от което две информационни точки А и В са в това отношение m. N (m ≠ п).
Решение. Ние избираме правоъгълна координатна система, така че точките А и В, намиращи се върху оста х симетрично около произхода и оста у преминава през центъра на AB (Фигура 4). Нека AB = 2a. След точка А има координира (а, 0), точка Б - координатите (-а, 0). Да предположим, че С принадлежи ни локус, координира С (х, у) и CB / CA = m / п. но средство
Ние трансформираме равенство. имаме
След разширяване скоби и намаляване на подобни термини, получаваме
Разделете лявата и дясната страна на това неравенство в (това може да се направи, тъй като по условие), след което изберете идеалното поле по отношение на х. получавам
Но последното уравнение определя окръжност с център и радиус Така, ако точката отговаря на изискванията на проблема, а след това той принадлежи (**).
От друга страна, се предполага, че координатите на точка (х, у) удовлетворяват уравнение (**). Правейки всички изчисления в обратната посока, пристигат в уравнението (*), което доказва, че нашата траекторията на точката.