вероятност плътност

Непрекъснато с. инча Можете да зададете функция, която се нарича разпределение на плътността или вероятност плътност, или функцията на диференциалното разпределение.

функция вероятност плътност при непрекъснато. инча X се нарича функция е (х) - първата производна на функцията на разпределение F (х):

От тази дефиниция следва, че функцията за разпределение е примитивното за разпределението на плътността.

За да се опише дискретни разпределението на вероятностите с. инча разпределение плътност не се прилага.

В вероятностни смисъла на разпределението на плътността.

По този начин, срокът на съотношението на вероятността, че непрекъснато стр. инча приема стойността принадлежащи на интервала (х, х + Δx), дължината на този интервал (когато Δx → 0) е равна на стойността на разпределението на плътността в точка х.

Функцията за плътност характеризира всяка стойност непрекъсната случайна променлива самостоятелно, а не набор както е случаят с функцията за разпределение.

Шанс да се удари с непрекъснато. инча при предварително определен интервал.

Според Нютон - Лайбниц:

Намирането на функцията за разпределение на функция известна плътност.

Поставянето на предходната формула А = -∞, б = х, и заместване на интеграция променлива х с т, имаме:

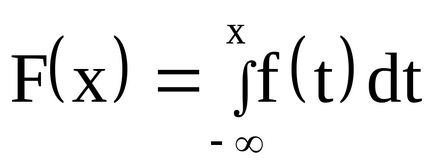
Свойства на плътността на вероятността

Собственост 1. Плътността на разпределение - отрицателен функция е (х) 0 (като кумулативна функция разпределение - без намаляване на функция, и плътността на разпределението на първото производно).

Доказателство. неадекватно неразделна

Той изразява вероятността случай че случайна променлива ще отчита стойността, принадлежащи към интервала (-∞, ∞). Очевидно е, че такова събитие е сигурно, следователно, вероятността за нейното единство.

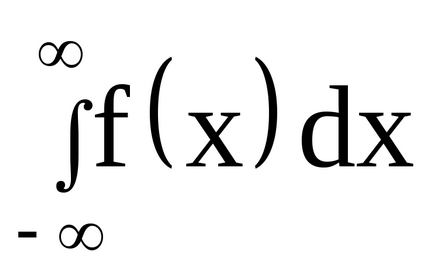
Геометрично това означава, че цялата площ на криволинеен трапец, ограничена от 0x на ос и кривата на разпределение е равен на единица.

Vchastnosti ако всички възможни стойности на случайната променлива принадлежат на интервала (А, В), на

.

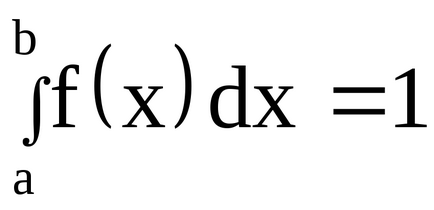
Възможна разпределение плътност график (пример)

f1 (х) - плътност на печелившата сума в първата игра

f2 (х) - плътност на печелившата сума във втората игра

Каква игра е за предпочитане?

Числени характеристики на случайни величини.

Тези характеристики дават възможност да се реши много проблеми, без да знае закона на разпределение на случайни величини.

Характеристики на случайна променлива позиция на реалната ос.

Очакванията за това е претеглена средна стойност на случайна променлива X, в която абцисата на всяка точка XI е включена в "тегло", равно на съответните вероятности.

Математическият очакването понякога се нарича просто като средната стойност на RV

За дискретна случайна променлива

За непрекъсната случайна променлива

Мода - е най-вероятната стойност на случайна променлива (т.е., за които разпределението на плътността на вероятността или пи F (х) достига максимума.).

Разграничаване унимодално разпределение (има един режим), мултимодален разпределение (има няколко режима) и animodalnye (не мода)