Закон за запазване на инерцията, кинетичната и потенциална енергия, силата на силите на физиката изпит

инерция на тялото

инерция на тялото е количество, равно на произведението на телесното тегло на скоростта си.

Трябва да се помни, че това е орган, който може да бъде представен като материална точка. инерция на тялото ($ р $) се нарича още инерция. Концепцията на инерция е въведена във физиката Рене Декарт (1596-1650). Терминът "импулс" се появи по-късно (impulsus в Латинска означава "тласък"). Инерция е количество вектор (и скорост) и се изразява с формулата:

инерция посока вектор винаги съвпада с посоката на скоростта.

На единица импулс в пулса SI приеме телесно тегло $ $ 1 кг, които се движат в $ $ 1 м / сек, следователно, устройството импулс е $ 1 кг $ $ $ · м / сек.

Когато тялото (материална точка) постоянна сила в продължение на период от време .DELTA.t $ $, а след това константа ще се ускори:

където $ ↖ $ и $ ↖ $ - начална и крайна скорост на тялото. Заместването на тази стойност в израза на втория закон на Нютон, получаваме:

Разширяване на скобите и използва израза за инерцията на тялото, ние имаме:

Тук $ ↖-↖ = Δp↖ $ - промяна инерция по време .DELTA.t $ $. Тогава предходната уравнението става:

Изразяване $ Δp↖ = F↖Δt $ е математическа нотация на втория закон на Нютон.

А работна сила за срока на нейната валидност, се нарича импулс сила. Затова промяната в точката на пулса е равно на импулса на промяна в качеството на нея.

Изразяване $ Δp↖ = F↖Δt $ нарича уравнението на движение на тялото. Трябва да се отбележи, че едно и също действие - точката за промяна на пулса - може да бъде получена от малка сила в продължение на дълъг интервал от време и голяма сила за малък период от време.

Инерцията на система от тела. Законът за промяна на инерцията

Инерция (количество на движение) на механичната система е вектор равна на сумата на импулси на материални точки на системата:

Законите и промени са следствие от опазване на инерция и третия закон на Нютон за втория.

Помислете за една система, състояща се от две тела. Force ($ F_ $ и $ F_ $ на фигурата, на системите на организма, с които си взаимодействат един с друг се наричат ​​вътрешни.

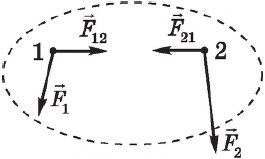
Да предположим, че в допълнение към вътрешните сили действат върху системата от външни сили, и $ $ $ ↖ ↖ $. За всеки орган може да напише уравнението $ Δp↖ = F↖Δt $. Сгъване на лявата и дясната страна на тези уравнения, получаваме:

Според третия закон на Нютон $> ↖ = -> ↖ $.

От лявата страна е геометричен сбор от промените в пулса на всички органи на системата, която е равна на промяна в инерцията на системата - $> ↖ $ .С оглед на това, равенството $ ↖ + ↖ = (↖ + ↖) ATi, $ може да се запише:

където $ F↖ $ - сумата на всички външни сили, действащи върху тялото. Този резултат означава, че системата за импулс може да се променя само от външни сили, системата е насочено промяна инерция, както и общата външна сила. Това е същността на правото на промяна на инерцията на механична система.

Вътрешните сили променят общата инерция на системата не могат. Те променят само импулсите на отделните органи на системата.

Закон за запазване на инерцията

От уравнение $> ↖ = F↖Δt $ следва закона за запазване на инерцията. Ако системата не се влияе от никакви външни сили, дясната страна на уравнението $> ↖ = F↖Δt $ изчезва, което означава постоянно общо инерция на системата:

Системата, за които не външна сила или резултантната на външните сили е нула, се нарича затворена.

Закон за запазване на моментните състояния:

Обобщение импулсни органи затворена система остава постоянна за всички взаимодействия между система от органи.

Резултатът е валиден за една система, съдържаща произволен брой тела. Ако сумата от външни сили не е нула, но сумата на техните прогнози за някаква посока е нула, системата на проекция на инерцията в тази посока не се променя. Например, система от органи на земната повърхност не може да бъде затворен поради силата на гравитацията, действащи върху цялото тяло, но количеството на прожекционни импулси в хоризонтална посока може да остане непроменен (при липса на триене), т. К. Посоката на тежестта сила не е действа.

реактивно задвижване

Да разгледаме примери, които потвърждават валидността на закона за запазване на инерцията.

Вземете детска гумена топка и пусна своя Наду. Ще видите, че когато въздухът започва да се излезе от нея по един начин, самата топката ще лети до друго. Ball движение е пример на реактивно задвижване. Това се обяснява с закона за запазване на инерцията: обща инерция "топка в себе си плюс въздух" преди изтичане въздуха е нула; той трябва да остане нула време на движение; обаче топката се движи в обратна посока на изхвърляне на струята, и с такава скорост, че неговата импулс модул равна на инерцията на въздушния поток.

Реактивен движение се отнася до движението на тялото, което се случва, когато се отделя от него със скорост на част от него. Благодарение на закона за запазване на инерцията на посоката на движение на тялото, докато обратната посока на отцепилата.

На принципа на реактивни базирани ракетни полети. Модерен космическа ракета е много сложен самолет. Мас ракета се състои от работен флуид маса (т. Е. Горещи газове, получени от горенето на гориво и изхвърлени като реактивен) и края, или се казва, че "сух" ракетата маса, оставащ след изхвърлянето на ракетата работен флуид.

Когато реактивната струя газ с висока скорост, изтласкан от ракетата, самата ракета тенденция в обратна посока. Според закона за запазване на инерцията, инерция $ m_ на

υ_p $, закупени ракети трябва да бъде равна на импулса $ m_ на · υ_ $ изхвърлени газове:

Това означава, че скоростта на ракета

Тази формула показва, че по-голяма е скоростта на ракетата, толкова по съотношението на скоростта на отработилите газове и течности маса работа (т. Е. Тегло на гориво) до края ( "сух") тегло на ракетата.

Формула $ υ_p = (> /) · $ υ_ е приблизително. Не се счита, че тъй като масата на горене летящи ракети става по-малко и по-малко. Точната формула за скоростта на ракетата се получава 1,897 К. Е. Tsiolkovskim и носи неговото име.

Циолковски формула ни дава възможност да се изчисли на резервите от горива, необходими за длъжностите, определени скорост ракети.

работна сила

Понятието "работа" е въведена в физика през 1826 г. от френския учен Жан Poncelet. Ако в ежедневието само човешки труд е работа по физика и по-специално в механиката се приема, че работата се извършва със сила. P. операция количество обикновено обозначен с буквата А $ $.

В работната сила - е мярка за силата в зависимост от неговия модул и посока, както и движението на точката на прилагане на силата. За постоянна сила и праволинейно движение на работата се определя от уравнението:

където $ F $ - сила, действаща върху тялото, $ Δr↖ $ - преместване, $ α $ - ъгълът между силата и обем.

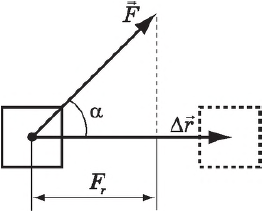
Работна сила, равна на произведението от сила и преместване модули и косинус на ъгъла между тях, т.е.. Д. Вътрешното произведение на вектори $ F↖ $ и $ Δr↖ $.

Заетостта - скаларното количество. Ако $ $ α 0, и ако $ 90 °