Базата за измерение на пространството за вектор и

Когато се обсъжда понятието п двумерен вектор и въведена в експлоатация на вектори, ние открихме, че множеството от всички N-двумерен вектори генерира линеен пространство. В тази статия ще говорим за най-важните понятия, свързани - от размера и основата на пространството за вектор. Също така, помисли теорията на разлагането на произволен вектор в основата и връзката между различните основи на п-тримерно пространство. Ние анализира в детайли конкретни примери за решения.

Навигация в страниците.

Концепцията за линейно пространство с размерност и основа.

Размерът на вектор пространство е броят е равен на максималния брой на линейно независими вектори в това пространство.

Основи на вектор пространство - подреден набор от линейно независими вектори в това пространство, броят на които е равна на размера на пространството.

Ето някои съображения, основани на тези определения.

Помислете за пространството на N-мерни вектори.

Ние показваме, че измерението на това пространство е равно на п.

Да вземем система от п единичен вектор на формата

Да приемем, тези вектори като редовете на матрицата А. В този случай, за матрица А е единична матрица с размери п към п. Рангът на тази матрица е равна на п (ако е необходимо, вижте статията ранг матрица: определяне, намирането техники). Следователно, системата на вектори е линейно независими, и тази система не може да се добави един вектор без да се нарушава нейната линейна независимост. Тъй като броят на вектори в системата равни п. измерение на пространството на N-двумерен вектори равна п. и единичен вектор образуват на базата на това място.

Последното твърдение и определянето на базата, можем да заключим, че всяка система за N-мерни вектори, броят на вектори, в които по-малко от п. Това не е основание.

Сега размените на първи и втори вектор система. Лесно е да се покаже, че полученият вектор система също е на основата на наш тримерно линейно пространство. Състав на матрицата, като неговите ред вектори на тази система. Тази матрица може да бъде получена от матрицата на идентичност чрез обмен на първата и втората линии, следователно, неговата ранг е равно на п. По този начин, системата на N линейно независими вектори и основа п тримерно пространство вектор.

Ако сменяте други вектори на системата, ние откриваме друг принцип.

Ако сте приели по-линейно независима система не е единичен вектор, тя е и основата на наш тримерно линейно пространство.

По този начин, вектор пространство на измерение п има най-много бази като има линейно независима система на п п двумерен вектори.

Ако говорим за двумерната вектор пространство (тоест, в самолета), неговата основа са всеки две трети-колинеарни вектори. Основа на триизмерното пространство са всеки три не-копланарни вектори.

Разполагате с няколко примера.

Дали са вектори на базата на триизмерна вектор пространство?

Векторите за разпадане в пространството на база вектор.

Нека произволни вектори са на базата на наш тримерно линейно пространство. Ако добавим към нея наш тримерно вектор х. получената система от вектори е линейно зависим. ние знаем, че най-малко един вектор е линейно зависима система се изразява по отношение на друга линейна, от линейна зависимост от свойствата. С други думи, най-малко един от векторите са линейно зависима система разделя останалите вектори.

Това ни води до един много важен теорема.

Всеки вектор п тримерно пространство вектор еднозначно разлага в основата.

Да - на базата на наш тримерно линейно пространство. Ние добави към тези вектори п двумерен вектор х. След това получената система от вектори е линейно зависим и вектор х може да бъде изразена линейно по отношение на вектори, където - някои номера. Така че ние сме получили разширяване на х в базата. Остава да се докаже, че това разлагане е уникален.

Да предположим, че има и друг разлагане, където е - някои цифри. Изваждане от лявата и дясната страна на последното равенство, съответно, от лявата и дясната страна на уравнението:

Тъй като системата от базови вектори е линейно независими, а след това по дефиниция линейната независимост на вектори, получени в резултат на половете е възможно само ако всички коефициенти равни на нула. Следователно, това, което е доказателство за уникалност разлагане вектор в базата.

Коефициентите се наричат ​​координатите на х в базата.

След запознаване с теоремата на разлагането на вектора в базата, ние започваме да разбираме същността на фразата "ние се дава наш тримерно вектор". Този израз означава, че ние считаме вектор х п двумерен вектор пространство, координатите на които са дадени в определена база. В същото време ние осъзнаваме, че един и същ вектор х към друга база на наш тримерно пространство вектор ще има координати, които са различни от.

Да разгледаме следния проблем.

Да предположим, че в някои основа на п двумерен вектор пространство ние дадена система на п линейно независими вектори

и вектор. Тогава векторите също са на базата на този вектор пространство.

Да предположим, че искате да намерите координатите на вектор х в базата. Ще означаваме тези координати, като.

х вектора в основата на представяне. Пишем това уравнение в координатна форма:

Това уравнение е еквивалентно на система от линейни уравнения н с п неизвестни променливи:

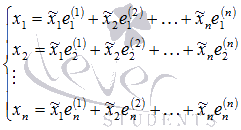
Обобщение на матричната система има формата

Ние означават с буквата А. Колоните на А са линейно независими вектори на вектори, така че ранга на тази матрица е равно на п. Поради своята детерминанта е различна от нула. Този факт показва, че системата има уникален разтвор, който може да се намери чрез всеки метод, например, чрез Kramer или метод матрица.

Тъй желаните координатите х в основата ще бъде намерен.

Нека разгледаме теорията с примери.

В основата на триизмерен вектор пространство даден вектори

Уверете се, че системата от вектори също е на базата на това място, за да намерите координатите на вектор х в тази база.

Системата за вектор е е необходимо на базата на триизмерна вектор пространство, така че да е линейно независими. Нека обясним това чрез определяне на ранга на А. редове са вектори. Място намери метод на Гаус

Следователно, Място (A) = 3. показва, че линейна независимост на вектори.

Така че, са в основата вектори. Нека тази основа вектор х има координати. След това, както са показани по-горе, връзката е определена от координатите на векторната система от уравнения

Опция е известно от стойности на условията, получаваме

Ние го реши от Kramer:

По този начин, вектор х има базисни координати.

.