функционални власт, неговите свойства и графики

Свойства на силови функции и техните графики

На следващо място, ние считаме, функцията за захранване
у (х) = х стр.

Функцията мощност с експонента равно на нула, р = 0

Ако експонентата на мощност функция у = х р е нула, р = 0. функцията мощност се определя за всички х ≠ 0 и е константа, равна на единство:






у = х р = 0 х = 1, х ≠ 0.

Функцията мощност с естествен нечетен експонента, р = п = 1, 3, 5.

Разглеждане на мощност функция у = XP = Xn с природен нечетен експонента п = 1, 3, 5. Този компонент може да се изписва като: п = 2k + 1, където к = 0, 1, 2, 3. - няма отрицателно число , По-долу са свойствата и графиките на тези функции.

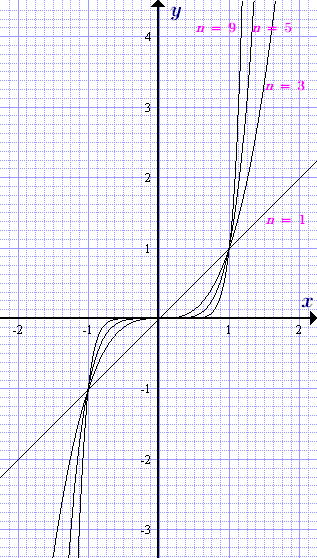
График мощност функция у = х п с природен нечетен индекс за различни стойности на експонентата п = 1, 3, 5.

Домейнът на определение: -∞ Наборът от стойности: -∞ Parity: странно, у (-x) = - у (х)
Еднообразието: нараства монотонно
Extremes: няма
Изпъкналостта:
при -∞ при 0 инфлексната точка: х = 0, у = 0
Точките на пресичане с координатните оси х = 0, Y = 0
граници на излагане:
;
Частни стойности:
когато х = 1,
Y (-1) = (-1) п ≡ (-1) 2k + 1 = -1
когато х = 0, Y (0) = 0, п = 0
когато х = 1, у (1) = 1, п = 1
Свържи се с функция:
когато п = 1. функция е обратна на себе си: X = Y
Когато п ≠ 1. корен е обратна функция на степен п.

Функцията мощност с естествен нечетен експонента, р = п = 2, 4, 6.

Разглеждане на мощност функция у = х р = х п дори с природен експонента п = 2, 4, 6. Такъв индикатор може да се изписва като: п = 2k. където к = 1, 2, 3. - положително. Имоти и графики на тези функции са дадени по-долу.

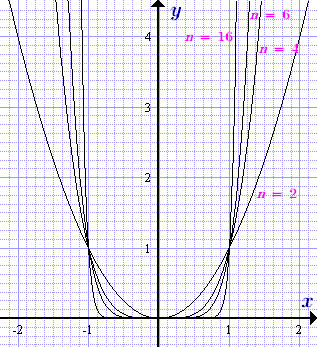
График мощност функция у = х п с природен експонента дори когато различни стойности на експонентата п = 2, 4, 6.

Домейнът на определение: -∞ Наборът от стойности: 0 ≤ Y <∞
Parity: още, Y (Х) = у (х)
монотонност:
в х <0 монотонно убывает
когато х> 0 монотонно увеличава
Силна: минимум, х = 0, Y = 0
Изпъкналостта: изпъкнала надолу
инфлексна точка: не
Точките на пресичане с координатните оси х = 0, Y = 0
граници на излагане:
;
Частни стойности:
когато х = 1. Y (-1) = (-1) п ≡ (-1) 2k = 1
когато х = 0, Y (0) = 0, п = 0
когато х = 1, у (1) = 1, п = 1
Свържи се с функция:
когато п = 2. корен квадратен от:
Когато п ≠ 2. корен на п.

Функцията мощност с отрицателен експонента, р = п = -1, -2, -3.

Разглеждане на мощност функция у = х р = х п с отрицателен експонента п = -1, -2, -3. Ако сложим п = к. където к = 1, 2, 3 - естествено, може да бъде представен като:

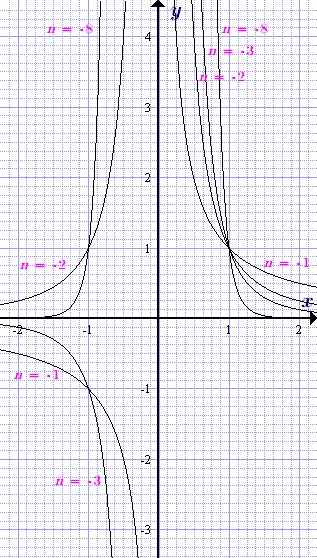
График мощност функция у = х п с отрицателен индекс за различни стойности на експонентата п = -1, -2, -3.

Нечетно индекс, п = 1, -3, -5.

Показани са свойства на функция у = х п нечетен отрицателен индексът п = -1, -3, -5.

определяне ОБЛАСТ: X ≠ 0
Наборът от стойности: ш ≠ 0
Parity: странно, у (-x) = - у (х)
Монотонността: намалява монотонно
Extremes: няма
Изпъкналостта:
в х <0. выпукла вверх
Когато X> 0. изпъкнала надолу
инфлексна точка: не
Пресечните точки с координатните оси: няма
подпише:
в х <0, y <0
когато х> 0, у> 0
граници на излагане:
; ; ;
Частни стойности:
когато х = 1, у (-1) = (-1) п = -1
когато х = 1, у (1) = 1, п = 1
Свържи се с функция:
когато п = 1.
за п <–2.

Дори индекс, п = -2, -4, -6.

Показани са свойства на функция у = х п с дори отрицателен индексът п = -2, -4, -6.

определяне ОБЛАСТ: X ≠ 0
Наборът от стойности: у> 0
Parity: още, Y (Х) = у (х)
монотонност:
в х <0. монотонно возрастает
Когато X> 0. намалява монотонно
Extremes: няма
Изпъкналостта: изпъкнала надолу
инфлексна точка: не
Пресечните точки с координатните оси: няма
Вход: у> 0
граници на излагане:
; ; ;
Частни стойности:
когато х = 1, у (-1) = (-1) п = 1
когато х = 1, у (1) = 1, п = 1
Свържи се с функция:
когато п = -2.
за п <–2.

Мощност функция с рационално (частична) индикатор

Разглеждане на мощност функция у = х р с рационално (фракционна) експонента. където п - цяло число, т> 1 - положително. При което, д, т нямат общ делители.

В знаменателя на фракционна индекс - нечетен

Да предположим, че знаменателя на фракционна експонента нечетен: M = 3, 5, 7. В този случай, стр функция мощност х се определя както от положителни и отрицателни стойности на аргумент х. Да разгледаме свойства като експоненциална функция, където р е индекс в рамките на определен обхват.

Отрицателни експонат р, р <0

Нека рационално степен (с нечетен знаменател m = 3, 5, 7) е по-малка от нула.

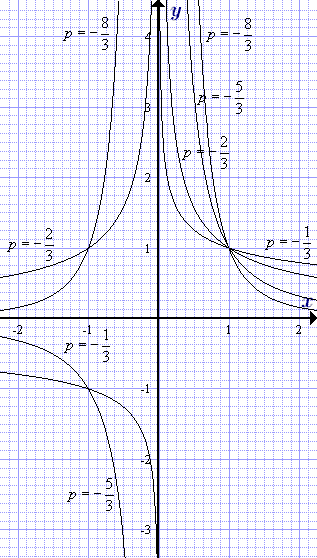
Графики на експоненциални функции с отрицателна рефракция рационално за различни стойности на експонентата. където m = 3, 5, 7 - нечетен.

Нечетно числител, п = 1, -3, -5.

Това са свойствата на мощност функция у = х р с рационално отрицателен индекс. където п = -1, -3, -5. - отрицателно нечетно число, m = 3, 5, 7 - нечетно число.

определяне ОБЛАСТ: X ≠ 0
Наборът от стойности: ш ≠ 0
Parity: странно, у (-x) = - у (х)
Монотонността: намалява монотонно
Extremes: няма
Изпъкналостта:
в х <0. выпукла вверх
Когато X> 0. изпъкнала надолу
инфлексна точка: не
Пресечните точки с координатните оси: няма
подпише:
в х <0, y <0
когато х> 0, у> 0
граници на излагане:
; ; ;
Частни стойности:
когато х = 1, у (-1) = (-1) п = -1
когато х = 1, у (1) = 1, п = 1
Свържи се с функция:

Дори числител, п = -2, -4, -6.

Свойства на мощност функция у = х р с рационално отрицателен индекс. където п = -2, -4, -6. - дори отрицателно число, m = 3, 5, 7 - нечетно число.

определяне ОБЛАСТ: X ≠ 0
Наборът от стойности: у> 0
Parity: още, Y (Х) = у (х)
монотонност:
в х <0. монотонно возрастает
Когато X> 0. намалява монотонно
Extremes: няма
Изпъкналостта: изпъкнала надолу
инфлексна точка: не
Пресечните точки с координатните оси: няма
Вход: у> 0
граници на излагане:
; ; ;
Частни стойности:
когато х = 1, у (-1) = (-1) п = 1
когато х = 1, у (1) = 1, п = 1
Свържи се с функция:

P положителен темп е по-малко от един, 0

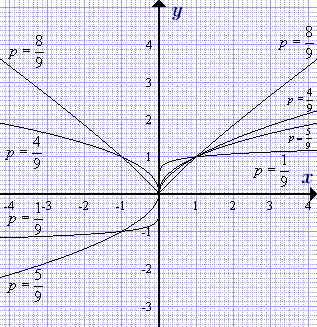
Графиката на функцията за захранване с рационално експонента (0

Нечетно числител, п = 1, 3, 5.

Свойствата на мощност функция у = х р с рационално индикатор. Ние сме в диапазона 0

Домейнът на определение: -∞ Наборът от стойности: -∞ Parity: странно, у (-x) = - у (х)
Еднообразието: нараства монотонно
Extremes: няма
Изпъкналостта:
в х <0. выпукла вниз
Когато X> 0. изпъкнала нагоре
инфлексната точка: х = 0, у = 0
Точките на пресичане с координатните оси х = 0, Y = 0
подпише:
в х <0, y <0
когато х> 0, у> 0
граници на излагане:
;
Частни стойности:
когато х = 1, у (-1) = -1
когато х = 0, Y (0) = 0
когато х = 1, у (1) = 1
Свържи се с функция:

Дори числител, п = 2, 4, 6.

Свойствата на мощност функция у = х р с рационално индикатор. Ние сме в диапазона 0

Домейнът на определение: -∞ Наборът от стойности: 0 ≤ Y <+∞
Parity: още, Y (Х) = у (х)
монотонност:
в х <0. монотонно убывает
Когато X> 0. монотонно
Силна: минимум при х = 0, у = 0
Изпъкналостта: изпъкнала нагоре, когато х ≠ 0
инфлексна точка: не
Точките на пресичане с координатните оси х = 0, Y = 0
Регистрирай се: ако х ≠ 0, у> 0
граници на излагане:
;
Частни стойности:
когато х = 1, у (-1) = 1
когато х = 0, Y (0) = 0
когато х = 1, у (1) = 1
Свържи се с функция:

Експонента р е по-голямо от едно, р> 1

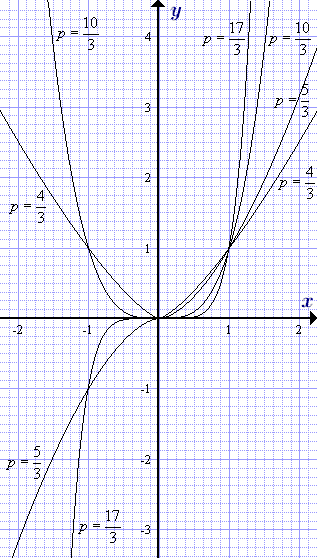
График функция мощност с рационално индикатор (р> 1) при различни стойности на експонентата. където m = 3, 5, 7 - нечетен.

Нечетно числител, п = 5, 7, 9.

Свойства на мощност функция у = х р с рационално степен по-голям от един. Когато п = 5, 7, 9 - нечетно число, m = 3, 5, 7 - нечетно число.

Домейнът на определение: -∞ Наборът от стойности: -∞ Parity: странно, у (-x) = - у (х)
Еднообразието: нараства монотонно
Extremes: няма
Изпъкналостта:
при -∞ при 0 инфлексната точка: х = 0, у = 0
Точките на пресичане с координатните оси х = 0, Y = 0
граници на излагане:
;
Частни стойности:
когато х = 1, у (-1) = -1
когато х = 0, Y (0) = 0
когато х = 1, у (1) = 1
Свържи се с функция:

Дори числител, п = 4, 6, 8.

Свойства на мощност функция у = х р с рационално степен по-голям от един. Когато п = 4, 6, 8 - още число, m = 3, 5, 7 - нечетно число.

Домейнът на определение: -∞ Наборът от стойности: 0 ≤ Y <∞
Parity: още, Y (Х) = у (х)
монотонност:
в х <0 монотонно убывает
когато х> 0 монотонно увеличава
Силна: минимум при х = 0, у = 0
Изпъкналостта: изпъкнала надолу
инфлексна точка: не
Точките на пресичане с координатните оси х = 0, Y = 0
граници на излагане:
;
Частни стойности:
когато х = 1, у (-1) = 1
когато х = 0, Y (0) = 0
когато х = 1, у (1) = 1
Свържи се с функция:

В знаменателя на фракционна индекс - дори

Да предположим, че фракционна знаменател на експонентата е още: m = 2, 4, 6. В този случай, функция х р мощност не е определено за отрицателни стойности на аргумента. Свойствата му са идентични със свойствата на функцията за захранване на степен ирационално (вж. В следващия раздел).

Мощност функция с ирационален показател

Разглеждане на мощност функция у = х р с ирационално експонента стр. Имоти тези функции се различават от по-горе, тъй като те не са определени за отрицателни стойности на аргумента х. За положителни стойности на аргумента, свойствата зависи само от стойността на експонентата р и не зависят от това дали р е цяло число, рационална.

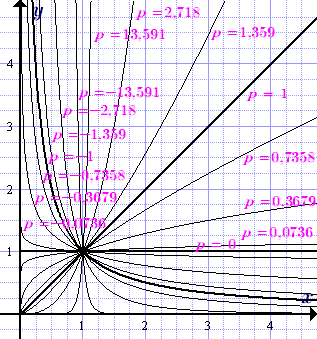
График мощност функция у = х р с ирационално индикатор за различни стойности на експонента п.

Мощност функция с отрицателен показател р <0

определяне ОБЛАСТ: х> 0
Наборът от стойности: у> 0
Монотонността: намалява монотонно
Изпъкналостта: изпъкнала надолу
инфлексна точка: не
Пресечните точки с координатните оси: няма
Ограничения :;
Конотацията: Когато х = 1, у (1) = 1, р = 1

Мощност функция с положителен показател р> 0

Индексът е по-малко от един 0

определяне ОБЛАСТ: X ≥ 0
Наборът от стойности: у ≥ 0
Еднообразието: нараства монотонно
Изпъкналостта: изпъкнала нагоре
инфлексна точка: не
Точките на пресичане с координатните оси х = 0, Y = 0
граници на излагане:
Частните значения: Когато х = 0, Y (0) = 0 р = 0.
Когато х = 1, у (1) = 1, р = 1

Голяма от един р> 1

определяне ОБЛАСТ: X ≥ 0
Наборът от стойности: у ≥ 0
Еднообразието: нараства монотонно
Изпъкналостта: изпъкнала надолу
инфлексна точка: не
Точките на пресичане с координатните оси х = 0, Y = 0
граници на излагане:
Частните значения: Когато х = 0, Y (0) = 0 р = 0.
Когато х = 1, у (1) = 1, р = 1