Как да намерите максималната или минималната на квадратна функция

В много задачи, необходими за изчисляване на максимална или минимална стойност на квадратна функция. Максималната или минимум може да се намери, ако първоначалното функция се записва в стандартната форма: е (х) = брадва 2 + BX + в + BX + C> или координатите на върха на параболата: е (х) = а (х - з) 2 + к + к>. Освен това, максималната или минималната всяка квадратна функция може да се изчисли чрез математически операции.

стъпки Редактиране

Метод 1 от 3:
Квадратна функция е написана по образец на правилата

Record функция в стандартна форма. Квадратна функция - функция уравнението на което включва променлива х 2>. Уравнението може или не може да включва променлива х. Ако уравнението съдържа променлива с експонента по-голямо от 2, той не описва квадратна функция. Ако е необходимо, да предостави подобни термини и да ги преместите да напише функция в стандартна форма. [1]

• Например, е дадена функция (х) = х + х 3 2 - х 2 х 3 + 2 + 4 + 3x ^ + 4>. Fold членовете на променлива х 2> и членовете с променливата х. да напише уравнението в стандартна форма:
  • е (х) = 2 х 2 + х 5 + 4 + 5x + 4>

Определя посоката на параболата. Графиката на квадратна функция е парабола. парабола клон насочен нагоре или надолу. Ако коефициентът на х 2> положителен парабола сочеща нагоре. Ако отрицателен коефициент, параболата е насочен надолу. Например: [2]

• е (х) = 2 х 4 + 2 х - 6 + 4x-6>. Тук, а = 2. така параболата сочи нагоре.
• е (х) = - х 3 х 2 + 2 + 8 + 2х + 8>. Тук а = - 3. така параболата надолу.
• е (х) = х 2 + 6 6>. Тук, а = 1. така параболата сочи нагоре.
• Ако параболата е насочен нагоре, за да я търси най-малко. Ако параболата е насочен надолу, търсейки своя максимум.

Вземете съответния F стойност (х). Заместник намерена стойност «х» в първоначалната функция за намиране на съответната стойност е (х). Така ще откриете минимална или максимална функция.

• В първия пример, е (х) = х 2 + 10 х - 1 + 10х-1> сте изчислено, че координатите на "х" е парабола връх х = - 5. Първоначалната функция на х заместител - 5. да се намери максималната си стойност:
  • е (х) = х 2 + 10 х - 1 + 10х-1>
  • е (х) = (- 5) 2 + 10 (- 5) - 1 10 (5) -1>
  • е (х) = 25 - 50-1
  • е (х) = - 26
• Във втория пример, е (х) = - 3 х 2 + 6 х - 4 + 6x-4> установите, че координата на "х" е връх на парабола х = 1. Първоначалната функция на х заместител 1. да се намери максималната си стойност:
  • е (х) = - 3 х 2 + 6 х - 4 + 6x-4>
  • е (х) = - 3 (1) 2 + 6 (1) - 4, 6 (1) -4>
  • е (х) = - 3, 6 + - 4
  • е (х) = - 1

Напишете отговора. Повторно се казва в изявлението на проблема. Ако е необходимо да се намери координатите на върха на параболата, запис отговор двете стойности х и у (или е (х)). Ако искате да се изчисли максималната или минималната на функция, в отговор да записва само стойността на у (или е (х)). За пореден път, погледнете знака на коефициент на. да потвърдите, че сте изчислили: на максимална или минимална.

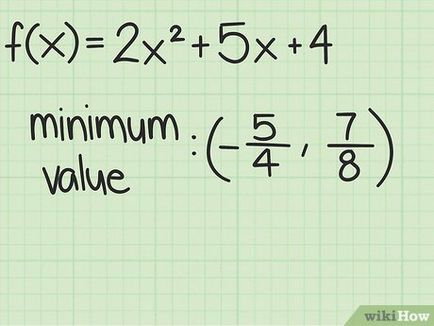
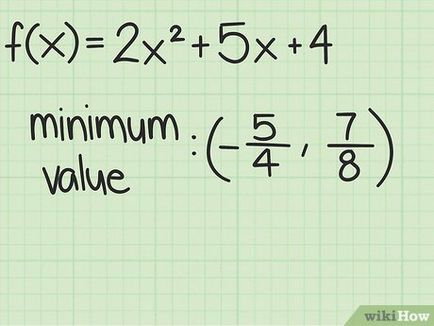
• В първия пример, е (х) = х 2 + 10 х - 1 + 10х-1> положителна стойност, така че да са изчислени минимум. парабола връх се намира в координатите (- 5 - 26). и минималната стойност на функцията е равна на - 26.
• Във втория пример, е (х) = - 3 х 2 + 6 х - 4 + 6x-4> отрицателна стойност, така че да се намери на максимум. парабола връх се намира в координати (1 - 1). и максималната стойност на функцията е равна на - 1.