Линейната зависимост на векторите
Определяне на линейната независимост на вектори
А1 вектори система. А2. Един нарича линейно независими. ако линейна комбинация от тези вектори λ1 * A1 + λ2 * А2 +. + Λn * равен на вектора нула само в нула набор от числа λ1, λ2. λn. което означава, че системата от уравнения: А1 + А2 x1 x2 +. Един + Xn = θ има само тривиално решение.
Проверете дали системата е линейно зависими вектори
1. Уверете се създаде система от уравнения:
2. Разрешете го от Гаус. Jordan система превръщане са изброени в Таблица 29.1. При изчисляване на дясната страна на системата, не се записват, тъй като те са нула и Йордания не са се променили в реализацията.
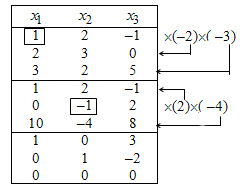
3. От последните три реда от таблицата, пише на системата за разрешителни за което е еквивалентно на оригиналната система:
4. Вземете общото решение:
5. Определяне по своя преценка стойност на свободната променлива X3 = 1, ние получаваме частния nontrivial разтвор X = (- 3,2,1).
A: Така ненулева набор от числа (-3,2,1) на линейна комбинация на векторите равно на нула векторни -3A1 + 2а2 + 1A3 = θ. Следователно, системата на вектори е линейно зависим.
Свойствата на векторни системи
Собственост (1)
Ако системата на вектори зависи линейно, а след това най-малко един от векторите разширени в другите и, напротив, ако поне един от векторите на системата може да се разшири до края, системата на вектори е линейно зависим.
Собственост (2)
Ако някои от подсистемата вектори са линейно зависими, а след това цялата система зависи линейно.
Имоти (3)
Ако системата е линейно независими вектори, а след това всяка подсистема е линейно независими.
Имоти (4)
Всяка система на вектори, съдържащи вектора нула е линейно зависим.
Собственост (5)
Системата на м двумерен вектори винаги е линейно зависим ако п е по-голям от броя на вектори на измерение (п> т)
система База вектор
R - броят на вектори, включени в основата.
Теорема 29.1 За базисни вектори система единица.
Ако системата е м двумерен вектори, съдържащи различни m единичен вектор E1 Е2. Ем. те са в основата на системата.
Алгоритъмът за намиране базисни система вектори
За да се намери на базата на вектори А1, А2. Едно е необходимо:
- Създаване на подходяща векторна система на хомогенна уравнения А1 + А2 x1 x2 +. Един + Xn = θ
- Носете тази система
