Векторът на магнитната индукция
дефиниция
характеристика на захранването е магнитно поле вектор на магнитната индукция $ \ overrightarrow $. Магнитна индукция вектор е основна характеристика на магнитното поле. Тя е равна на силата на граничните връзки, с които магнитните силови действа на елементарни ток ($ IDL $) към продукта на текущата $ (I) $ и размера на елемента за направляване ($ дл $):
индукция вектор е насочен перпендикулярно на елементарен ток (или повече каже проводник елемент ($ \ overrightarrow $)) от (1) и перпендикулярна на посоката на силата, която действа върху част от магнитното поле.
Ако $ \ overrightarrow $ = конст, а след това на магнитното поле се нарича хомогенна. Ако магнитното поле е постоянна във времето, той се нарича постоянен.
Понякога величината на индукцията на хомогенно магнитно поле се определя като:
където $ M_ $ - максимален въртящ момент, действащ върху линия с ток, който се поставя в магнитно поле, $ = p_m е $ - магнитен момент верига ($ S $ - контур площ). За посоката на вектора на $ \ overrightarrow $ вземе посоката, в която областта е установен от действието на положителното нормално да течение на ток. Във всеки случай, те казват, че магнитната индукция вектор е насочен по посока на постъпателно движение на десния винт, ако тя се върти в посоката на тока във веригата.
Много често, определението за вектора на магнитната индукция изписва така:
Решете контрол по всички предмети. 10 години опит! Цена от 100 рубли. период от 1 ден!
където $ \ overrightarrow $ - сила, действаща върху елемента с ток. В този случай, ако прав проводник и магнитна индукция е постоянна във всички точки, с формула (2) могат да бъдат трансформирани в израза:
индукция Модул вектор може да бъде определено, както и въз основа на силата на Лоренц ($ \ $ overrightarrow), която действа върху движеща се със скорост $ \ overrightarrow заредена частица $ (зареждане р) в магнитно поле:
Основната единица за измерване на магнитната индукция в системата SI е тесла (Т).
Принципът на наслагване на вектора на магнитната индукция
Емпиричните доказано, че магнитното поле се извършва принцип суперпозиция:
Ако магнитното поле се генерира от редица ток (движещи се заряди), тя е равна на вектор сбора на отделните области:
Задача: Проводникът е квадрат, чиято страна е равна на г, на силата на тока, протичащ през I. Намерете го на магнитното поле в точката на пресичане на диагоналите на квадрат.
Да приемем, че проводник равнина съвпада с равнината на Фигура 2. Ние определяме посоката на теченията.
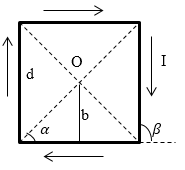
В точка O магнитното поле създава четири поредни диригент. Напрежението четирите полета са насочени в съответствие с дясна ръка винта произнесе нас, перпендикулярна на равнината на фигурата. Следователно, вектор Сумата от областта в принципа на суперпозиция се заменя с алгебрични, пишем:
И на симетрия, очевидно е, че всички модули индукциите са равни, тогава можем да запишем, че:
В "електромагнетизъм" сме намерили формулата за изчисляване на единица на магнитната индукция линеен проводник с ток. Когато се прилага към нашия случай модул $ \ $ overrightarrow ще изглежда така:
\ [B_1 = \ frac_0I> \ наляво (COS \ алфа -cos \ р \ дясно) \ наляво (1.3 \ полето), \]
ъглите $ \ алфа $ и $ \ бета $ са показани на фигура 1. В (1.3) $ \ бета = \ пи - \ а \ до COS \ бета == - защото \ алфа $ пренаписване (1.3) .:
Тъй като ние се занимаваме с площада, ние отбелязваме, че :. $ B = \ Фрак, \ алфа = \ Фрак \ до защото \ алфа = \ Фрак> $ заместване в (1.4), това, което сме получили и (1.4) заместваме в (1.2), трябва:
Цел: безкрайно дълъг проводник, носещ ток (I) е огъната под прав ъгъл (Фигура 2). Виж магнитното поле в точка А, която е показана на фиг. 3.

В точка А, областта е създадена от две части на проводника:
Помислете за един хоризонтален участък, който се намира върху продължаването на точка А. Тази част на проводника с ток генерира поле в точката A индукция $ (\ overrightarrow>) $, което е равно на нула, тъй като в точка А между ъглите на всички елементи, с ток и вектори радиус са равна на $ \ пи \ Следователно $, вектора на продукта ($ \ наляво [г \ overrightarrow \ overrightarrow \ полето] $), в биологична практика - Savar - Лаплас нула .:
където $ \ overrightarrow $ - радиус вектор, съставен от елемента ток $ Id \ overrightarrow $ до точката, в която се търси на магнитното поле ($ \ $ overrightarrow).
Предизвикване на магнитното поле на безкрайно прав проводник, носещ ток (I) в точка А ще бъде равен на:
Ние имаме полу-безкраен проводник, следователно, на принципа на суперпозиция, ние откриваме, че нашият диригент индукция е: