въртенето на тялото - studopediya

Тя се нарича тяло цилиндър, който се състои от два кръга, които не лежат в една равнина и над друг паралелен превод, както и всички сегменти, свързващи съответните точки на тези кръгове.

Кръгове се наричат ​​основи на цилиндъра, а отсечката, свързваща цилиндъра.

Тъй като паралелно предаване е движението, на базата на цилиндъра са равни.

Тъй като паралелен трансфер равнина стане успоредна равнина (или да се), след това на базата на лъжата на цилиндрите в успоредни равнини. Тъй паралелни точки за трансфер се измества паралелно (или съвпадат) за насочване на същото разстояние, след това образуване на цилиндъра са успоредни и равни.

повърхност цилиндър се състои от основи и повърхността на страничната. Страничната повърхност се състои от генератори.

Цилиндърът се нарича директен ако неговите генератори перпендикулярна на равнината база.

радиус цилиндър се нарича радиус на основата му. Височината на цилиндъра е разстоянието между равнините на нейните основи. Оста на цилиндъра се нарича права линия, минаваща през центъра на основата. Това е по паралелен начин.

Cone е орган, който се състои от кръг - основата на конуса, не точките лежи в равнината на този кръг, - върха на конуса и всички сегменти, свързващи върха на конуса с базовите точки.

Сегменти, свързващи върха на конуса с база кръг tochkami наречени конус генератори. Повърхността на конуса се състои от основа и странична повърхност.

А конус се нарича директен ако отсечката, свързваща горната част на конуса с базовия център.

Височината на конуса се нарича перпендикуляра падна от срещата на високо равнище на основната равнина. В дясната височина конус база съвпада с базовия център. Ос на прав кръгов конус се нарича ред, съдържащ разгара си

Наречен топка орган, който се състои от всички точки в пространството на разстояние не по-голямо това, от тази гледна точка. Тази точка се нарича център на света, а това разстояние е сфера с радиус.

топка гранична повърхност, наречена топка или сфера.

Следователно, точките на сфера са всички точки на играта, които са отстранени от центъра на разстояние равно на радиуса. Всеки сегмент, свързваща центъра на сферата с точката на сферична повърхност, също наречена радиус.

Сегмент свързване на две точки от сферична повърхност, минаваща през центъра на диаметъра на топката се нарича. Краищата на всеки диаметър се наричат ​​диаметрално разположени точки на земното кълбо.

Ball, както и един цилиндър и конусовиден е орган на революцията. Той се получава чрез завъртане на полукръг около нейния диаметър като ос.

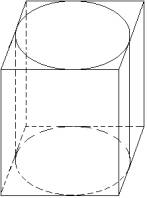
Prism нарича вписан цилиндър, ако неговите основни редовни полигони вписани в основата на цилиндъра, и страничните ръбове се образуват в цилиндъра.

Prism нарича описано около цилиндъра, ако Ба, наличието на него - е описан полигони близо до долната част на цилиндъра и страничните части на съответния цилиндър.

Топката или сферична повърхност е локус на точки в пространството-ва отдалечена от дадена точка O (център) на предварително определени разстояния зададена R (радиус). Всички пространството във връзка с този ша rovoy повърхност разделена на vnut-rennyuyu област (която може да бъде от свързващ конец и точка от повърхността) и външна. Първият от тези области се нарича ОЗНАЧАВА-топка. Така, топката - мястото на всички точки на разстояние от желаната точка O (центъра) в зададени разстояния, които не надвишават определена стойност R (радиус). Ball повърхност Jav-желае да се създаде границата, разделяща топката от район около Руж.

Сферична повърхност и топката може да се получи чрез завъртане на кръга (кръгче) около един от диаметрите.

Да разгледаме окръжност с център О и радиус R (фиг. 1), който се намира в равнината Ya-STI Ние го върти около диаметър AB. След това всяка от кръга на точки, като М, в червено-Oche описва по време на въртенето кръг с централната си точка M0 проекцията на въртящ момент М на въртене ос депозитите на AB на. Равнината на кръга, перпендикулярна на оста на въртене. ОМ радиус водещ от центъра на първоначалния кръг точка М ще запази размер по време на целия Vera-scheniya, и тъй като точка M по всяко време ще бъде разположен на сфера повърхност симетричен с център О и радиус R. повърхност топка може да бъде получена чрез завъртане на кръга около някой от неговите диаметри.

Топката е как тялото се получава чрез завъртане на кръга; ясно е, че за всичките топката достатъчно, за да се върти около полукръг ограничаване на нейния диаметър.